Welcome!
This site is a collection of interactive demos covering selected Computer Graphics topics.
Curve Demos
In modeling software, there is usually some kind of tool that allows users to define smooth, curved shapes. But how exactly does the computer draw them? A common approach is using so-called parametric curves. A selection of such curves is discussed in the demos of this section.
To get the most out of the demos, I recommend going through them in the order provided. A great introduction into the beauty of curves is this awesome video by Freya Holmér. For more detailed mathematical background on the topics discussed I can recommend the lecture notes of CS3621 at Michigan Technological University.
Bézier Curve Intro
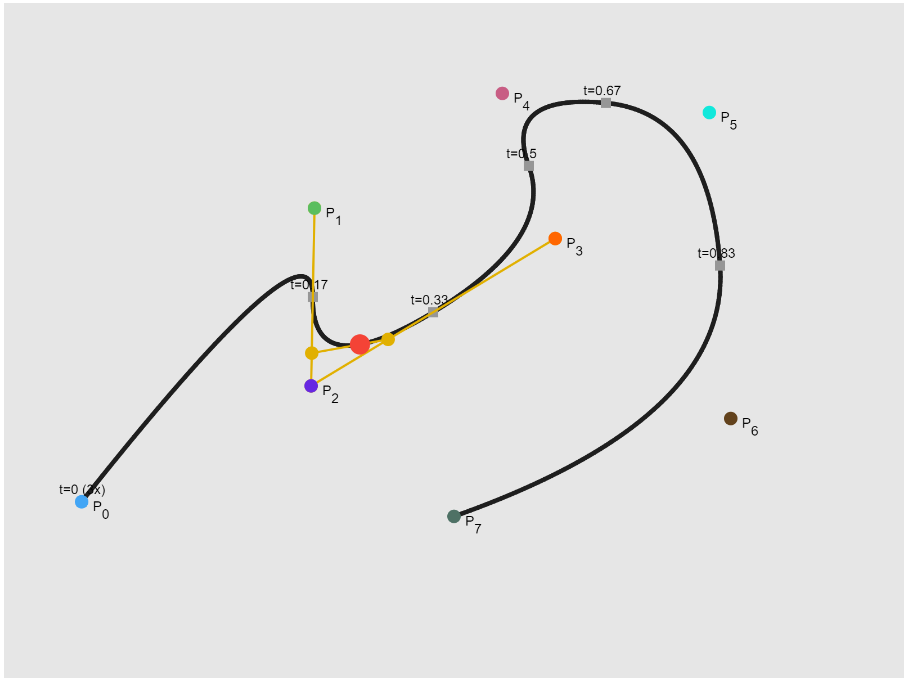
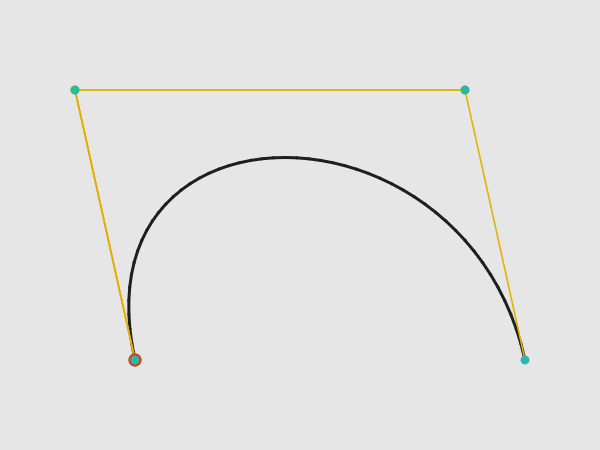
Bézier curves are arguably the most well-known and widely used type of parametric curve. This demo explains the idea behind Bézier curves from the ground up. You will also learn about De Casteljau's algorithm that is used for drawing Bézier curves along the way.
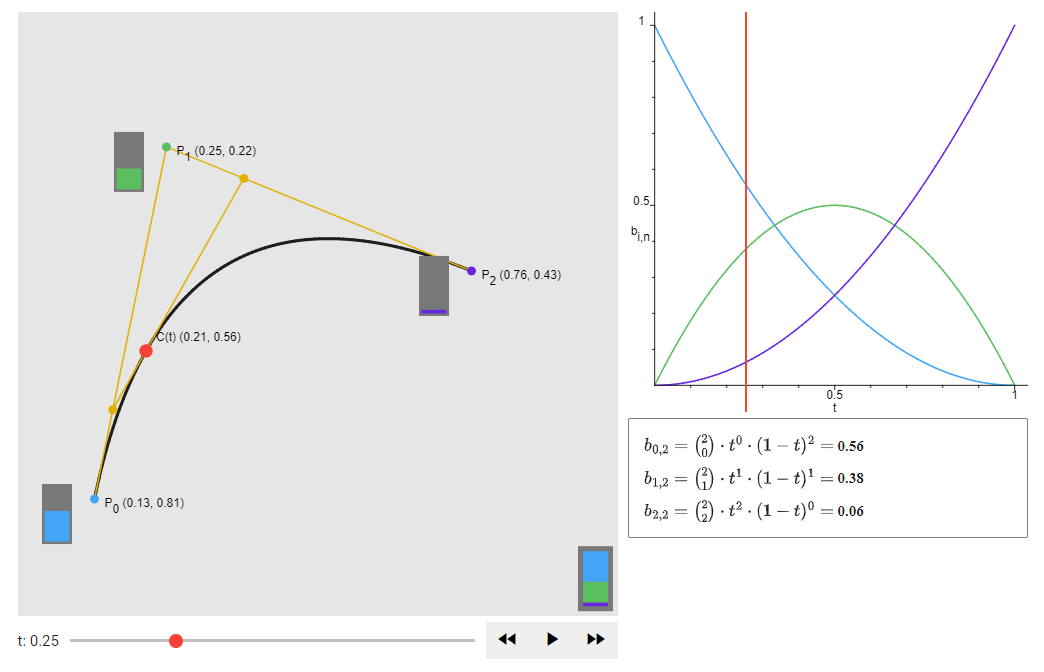
Bernstein Polynomials
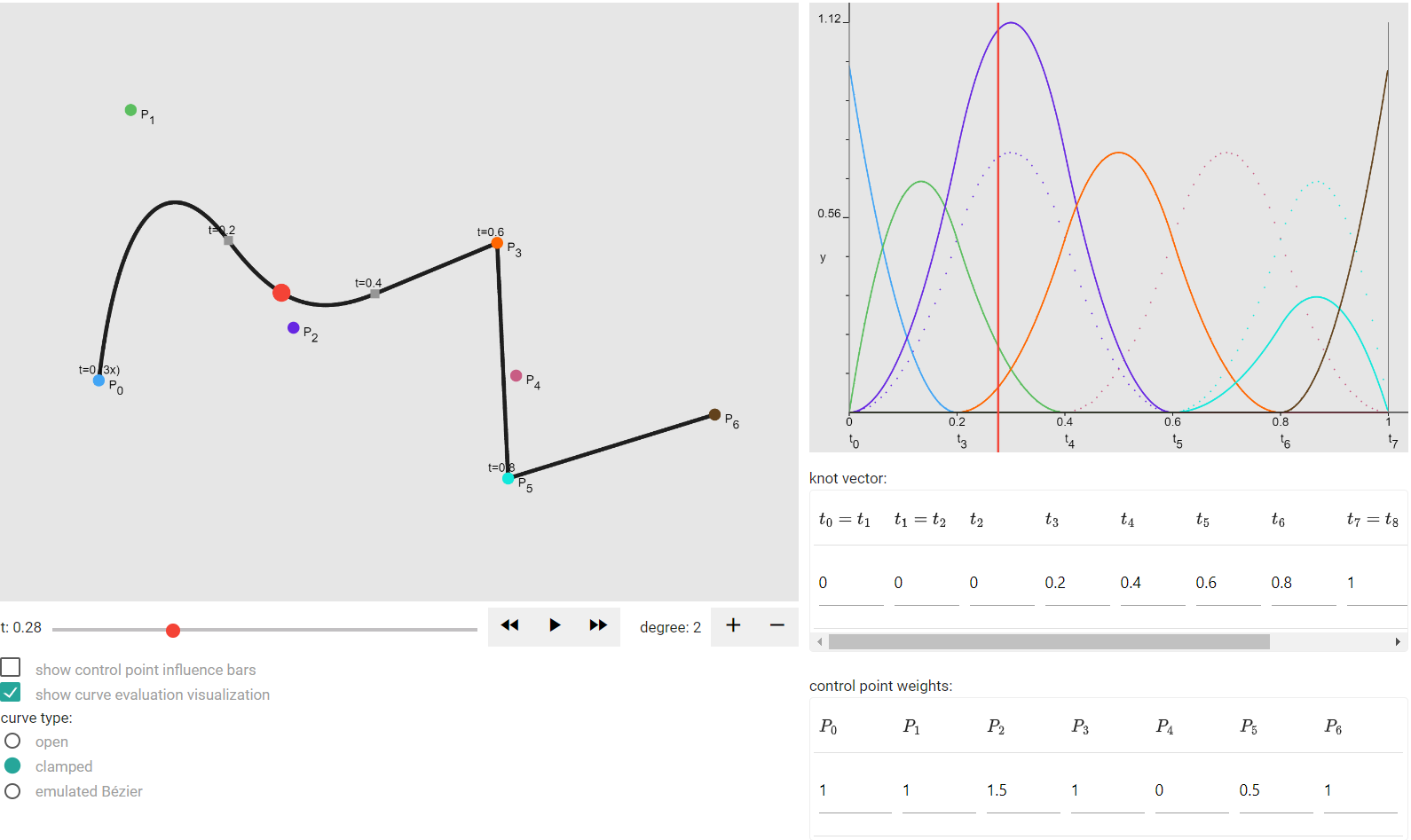
This demo helps you understand, how exactly the control points of the Bézier curve influence its shape. You will learn about the so-called Bernstein polynomials that define each control point's influence on the curve shape.
Other Topics
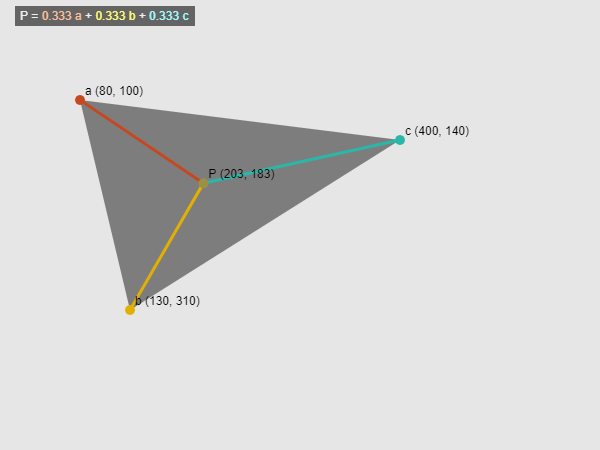
Barycentric coordinates
Barycentric coordinates allow one to define the position of points along the surface of a triangle (independent of the concrete position of the three points the triangle consists of). This has many useful applications in Computer Graphics, mainly in rendering. This demo should help you get an intuitive understanding of how barycentric coordinates work.